Huffman Compression

Git repository unavailable.

I normally wouldn't talk about any course projects but this was a small one and I thought it was pretty cool.

Students who have taken an introductory programming class have probably heard of or been asked to implement Huffman codes for file compression. This is for good reason: it allows a student to define their own implementation for a simple binary tree data structure (for n-ary implementations of Huffman encodings), and potentially makes use of some clever recursion. There are plenty of resources online but I aim to just provide a simple and concise explanation.

What is a Huffman code?

At a high level, a Huffman code is a way of encoding data (in our case, using 1s and 0s) by reducing the length of a code associated with more frequently appearing characters, and having longer codes only for less common characters. This can be visualized as a tree of frequencies and characters.

How is this tree formed?

Here is an example of a Huffman tree for the word "assassin":

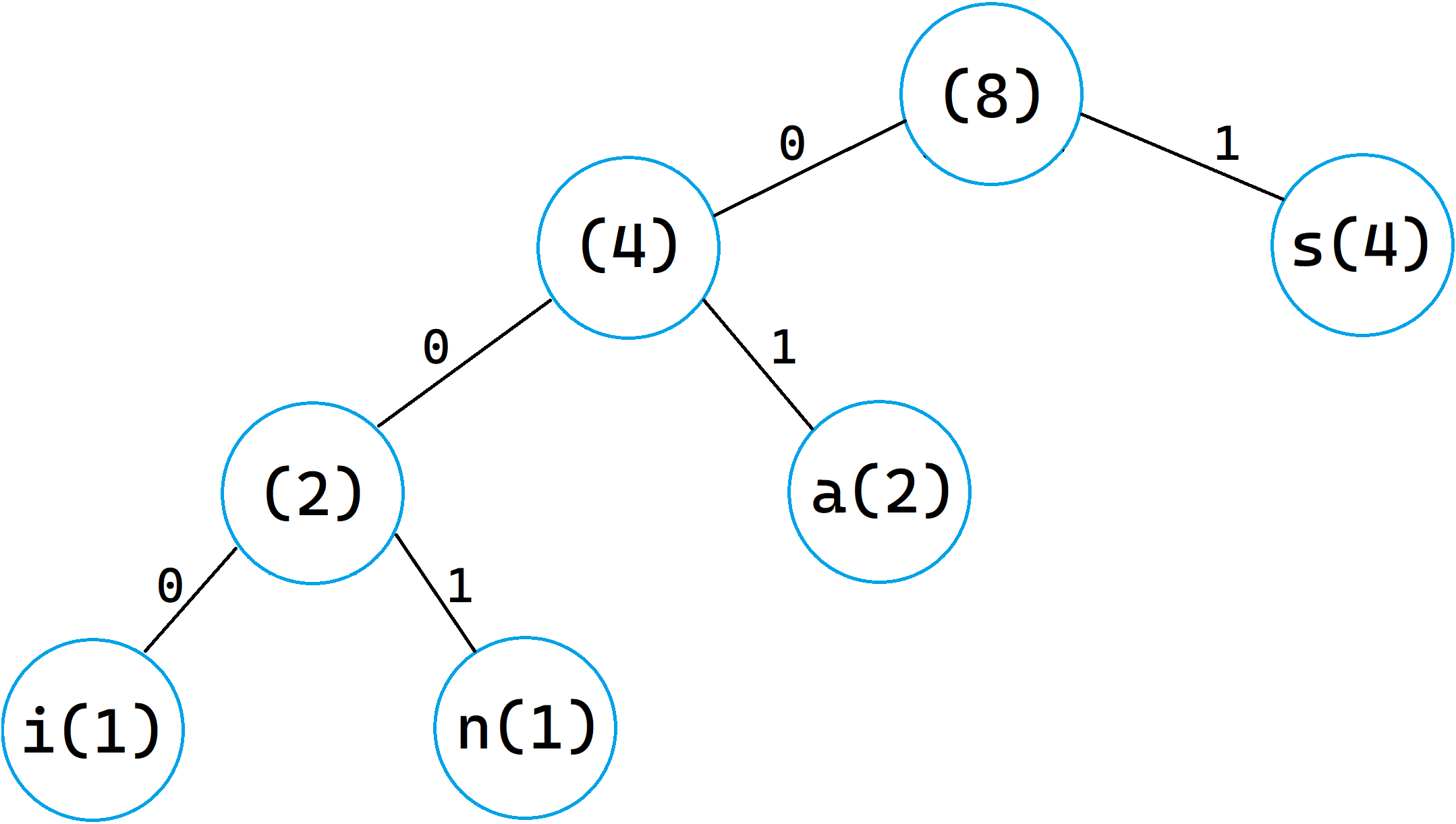
Each non-leaf node contains the total frequency of the nodes below it, and each leaf contains a character, and its frequency. The path to each leaf is the code for the character, with the left "branch" representing a 0, and the right representing a 1. Notice how the path to more frequently-appearing characters is shorter, and vice versa; the code for 'a' is just "1", while the code for 'n' is "001".

Why is this better than the what a computer normally does?

In standard ASCII encoding, each character is encoded by 8 bits which is equivalent to 1 byte. Each bit is either a 0 or a 1, with a lowercase a, for example, being 97, or 01100001 in bits (binary). Therefore, in standard ASCII, the word "assassin" takes 64 bits of space. On the other hand, our Huffman code only takes 2 bits of space to encode an a, 1 bit to encode an s, and 3 bits each for i and n. Using the encoding we have devised, the number of bits needed to represent "assassin" is reduced to only 14.

In practice, this requires another file to actually store the encoding scheme, so that you can decode the file after it has been compressed. But, the size of that file can only be so large, bounded by the actual number of characters that ASCII can represent (256). So as you increase the size of the data you are compressing, the size of the decoder file increases more slowly, and only up to a certain point. This makes Huffman compression, to an extent, more useful as you increase the size of the file you are compressing.

Read more about Huffman codes.